Геометрия | 5 - 9 классы
На рисунке угол BCA = 135°, АС = 9см , ВD = 5 см.
BD перепендикулярен AD.
Найдите площадь ABD.

В треугольнике ABC найдите угол B, если известно, что?
В треугольнике ABC найдите угол B, если известно, что.

1. Найдите и укажите, чему равен КАЖДЫЙ угол при двух параллельных прямых и секущей, если угол 2 = 85°?
1. Найдите и укажите, чему равен КАЖДЫЙ угол при двух параллельных прямых и секущей, если угол 2 = 85°.
Помогите пожалуйста.

Внешний угол треугольника равен 140 градусам?
Внешний угол треугольника равен 140 градусам.
Найдите сумму двух внутренних, не смежных с ним.
И если можно с пояснением).

Пожалуйстаа плизз помощьВ треугольнике АВС высота ВК является и биссектрисой угла АВС?
Пожалуйстаа плизз помощь
В треугольнике АВС высота ВК является и биссектрисой угла АВС.
Найдите угол В и угол С, если угол А = 50.

Дано :ABCD — параллелограмм ;∢ BCA = 43° ;∢ BAC = 31°?
Дано :
ABCD — параллелограмм ;
∢ BCA = 43° ;
∢ BAC = 31°.
Параллелограмм 8.
Png
Найти :
∢ BAD =
° ; ∢ B =
° ;
∢ BCD =
° ; ∢ D =
°.

Найдите площадь параллелограмма, изображённого на рисунке?
Найдите площадь параллелограмма, изображённого на рисунке.

❗СРОЧНОООО❗19?
❗СРОЧНОООО❗
19.
7. найдите площадь сечения правильной шестиугольной пирамиды.

В треугольнике ABC угол A равен 80 градусам, а угол C на 30 градусов меньше угла B?
В треугольнике ABC угол A равен 80 градусам, а угол C на 30 градусов меньше угла B.
Найдите углы B и C.

Найдите внешний угол при Третьей вершине треугольника если два других угла равны ?
Найдите внешний угол при Третьей вершине треугольника если два других угла равны .

Дан параллелограмм авсд один угол 50° второй 85° найти наименьший угол ?
Дан параллелограмм авсд один угол 50° второй 85° найти наименьший угол .
На странице вопроса На рисунке угол BCA = 135°, АС = 9см , ВD = 5 см? из категории Геометрия вы найдете ответ для уровня учащихся 5 - 9 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.

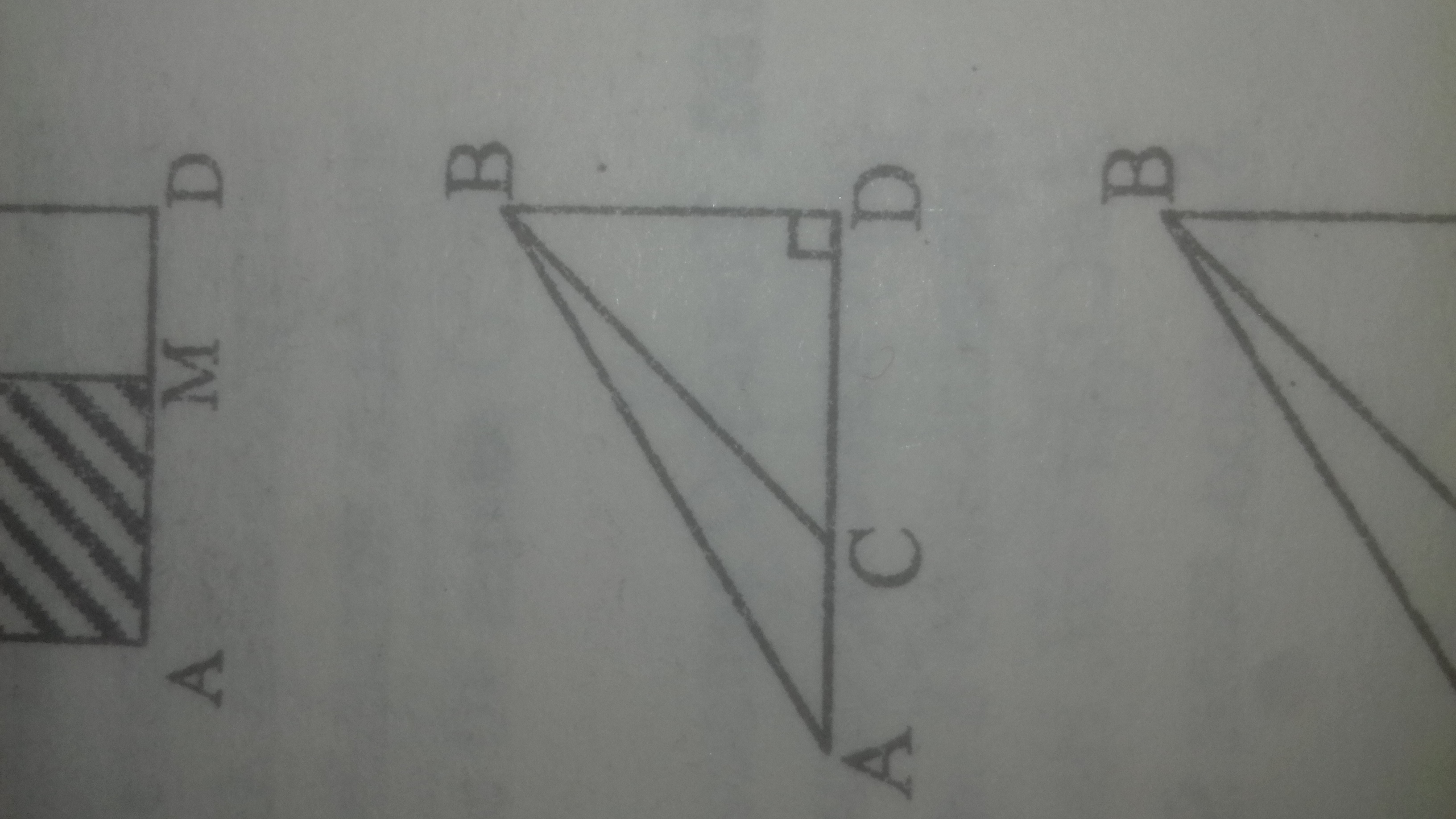
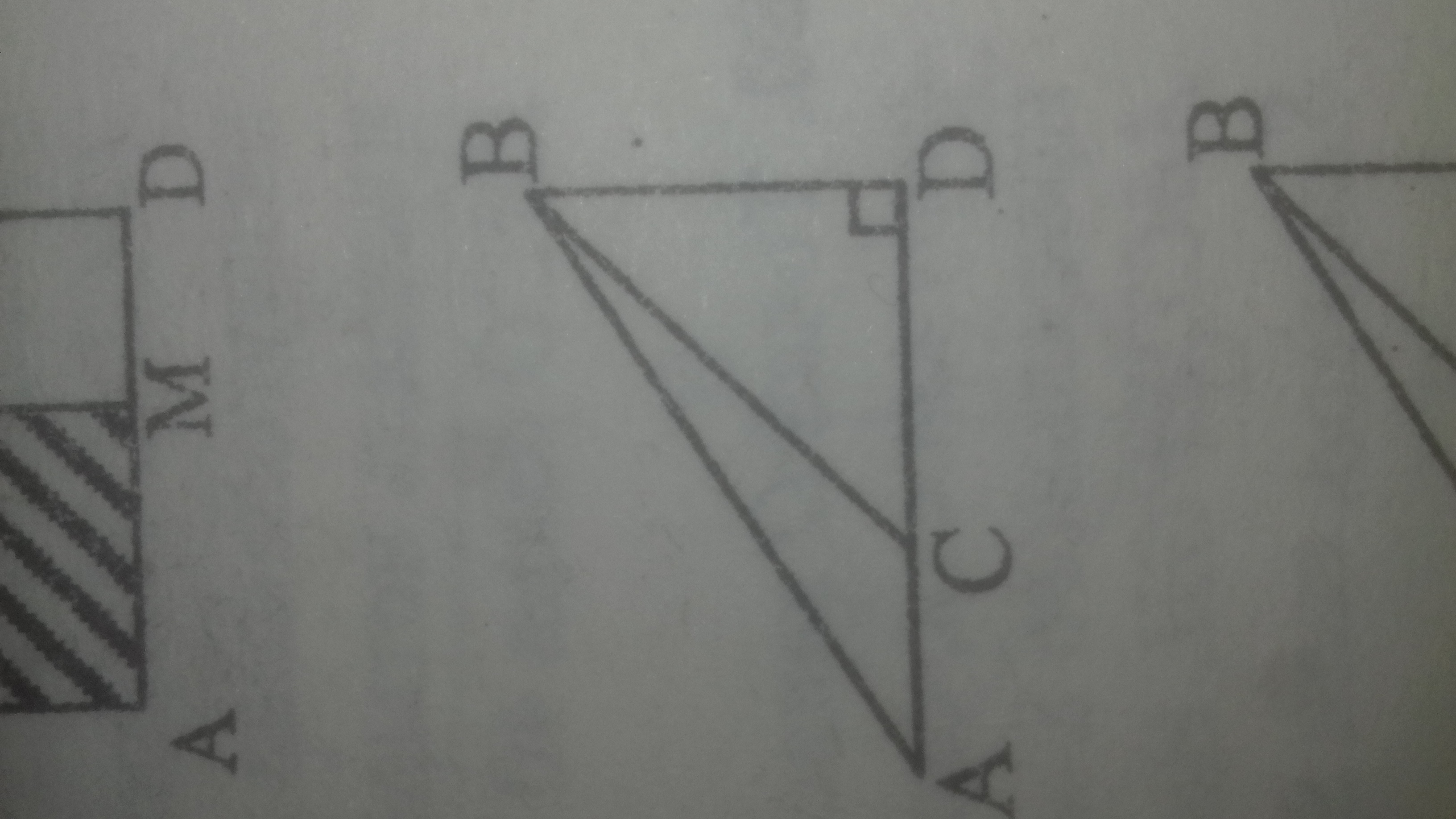




∠DFC = 135° ⇒ ∠BCD = 180° - 135° = 45°
ΔBCD : ∠BDC = 90° ⇒ ∠CBD = 90° - 45° = 45°⇒ΔBCD - равнобедренный и BD = CD = 5 см
АD = АC + CD = 9 + 5 = 14 cм
S(ΔABD) = 1 / 2·AD·BD = 1 / 2·14·5 = 35.